2.3 Construction d’un tétraèdre :

Précédemment, un cube a été construit en saisissant les coordonnées de ses sommets, mis il n’a pas été construit. Si l’on modifie la position de l’un de ses sommets à la souris, ce n’est plus un cube.

Dans ce qui suit, nous allons construire un tétraèdre régulier en utilisant ses propriétés géoémtriques.

Conceptuelisation :

• Construire un triangle équilatéral qui servira de base.
• Construction du centre de gravité de ce triangle
• Constructtion des sommets du tétraèdre.

Pour construire un triangle équilatéral, il nous faut un plan, par exemple le plan (xOy).

• Construisons les points de coordonnées (0, 0, 0), (1, 0, 0), (0, 1, 0).
• Construisons le plan passant par ces trois points :
• Cachons les trois points de base pour éviter de les déplacer par accident. On pourrait également fixer leurs coordonnées.

Le résultat doit ressembler à ceci :

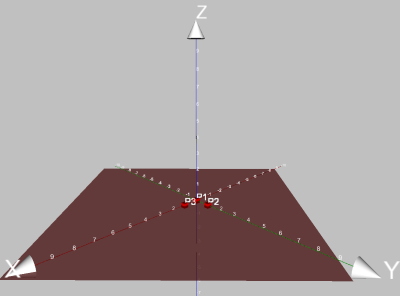
Tournons maintenant la figure de manière à se placer au-dessus du plan.

on construit maintenant deux points dans le plan : sélectionner le plan et cliquer sur l’icône ’Point’. On aurait également pu sélectionner le plan et faire un double clic droit hors du plan. IL faut enfoncer la touche ALT pour pouvoir faire un double clic droit dans le plan. Enfin, on aurait sélecctionner le plan et faire ALT-P.

Déplaçons les points pour obtenir ceci :

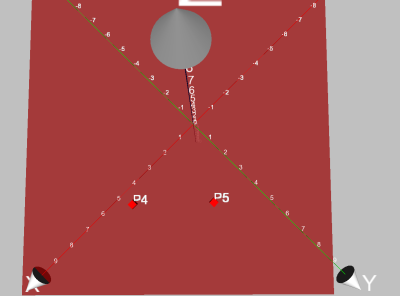
En construisant deux cercles, on construit le troisième sommet du triangle de base.

Sélectionner deux points ne suffit pas à définir un cercle dans l’espace. Il faut de plus indiquer le plan contenant le cercle.

On obtient donc ceci :

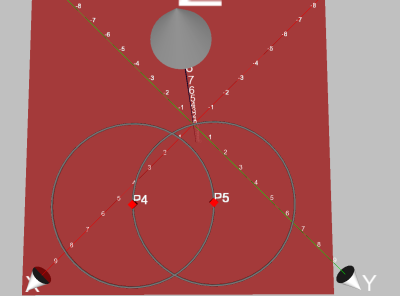
Sélectionner les cercles et faire ALT-P pour construire les points d’intersection.

On peut ne garder qu’un seul des deux points d’intersection puis cacher les deux cercles.

Construire maintenant les segments reliant les sommets. Pour cela sélectionner les sommets et cliquer sur l’icône Segment. ²

Construisons maintenant le centre de notre triangle équilatéral. Une méthode est :

• Selectionner deux sommets et cliquer sur l’icône ’Point’ ce qui construit le milieu.
• Relier ce point au sommet opposé pour obtenir une médiane médiane du triangle. Recommencer avec un autre côté du triangle puis construire l’intersection des deux médianes.

  

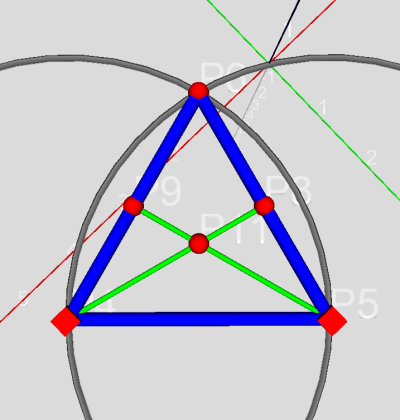
Maintenant, deux conditions doivent être réalisées :

1. Tous les sommets sont à égales distance les uns des autres.
2. Le quatrième sommet se trouve sur la perpendiculaire au plan de base passant par le centre du triangle que l’on vient de construire.

Pour construire cette perpendiculaire, sélectionner le centre du triangle puis le plan et cliquer sur l’icône ’Droite’. . Le quatrième sommet se trouve sur cette droite. ³.

Construisons maintenant la sphère de centre P4 passant par en sélectionnant P4 puis P5 et en cliquant sur l’icône ’Sphère’.

Construire maintenant le point cherché en sélectionnant la sphère et la droite et en cliquant sur l’icône ’Point’.

Cacher maintenant les objets inutiles, dessiner les faces pour obtenir quelque chose comme :

2.3.1 Ajouter une texture

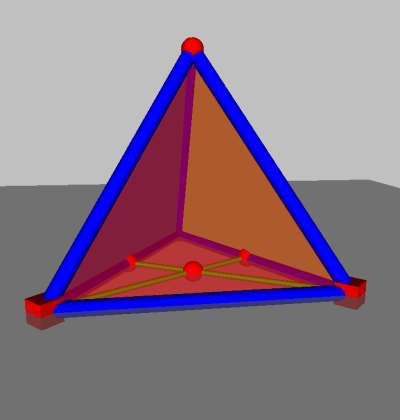
Passez ce paragraphe si seul l’aspect géométrique de la construction vous intéresse.

Cherchez une image de la pyramide de Gizeh.

En voici une libre de droits :

Cette image peut être utilisée pour décorer les faces de notre tétraèdre. Voici comment :

• Enregistrer l’image dans le dossier de votre choix.
• Faire un clic droit sur un des triangles > Couleur Taille et Texture > Onglet texture.
• Select ?Choose 10 texture ?
• Choisir l’image qui vient d’être enregistrée.

Ici, Archimède rappelle que la construction en cours doit être enregistrée pour pouvoir continuer. En effet, Archimède va sauvegarder la texture dans le même dossier que la figure qui donc être connue au moment où elle est appliquée.

Si une image porte le même nom, Archimède demande si l’ancien fichier doit être remplacé par le nouveau.

Si tout va bien, la face du tetraèdre doit ressemblé à ceci :

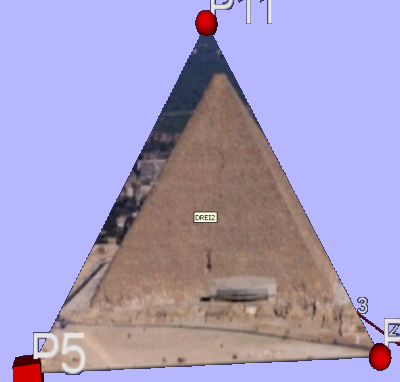
Si c’est le cas, not , choisir alors l’une des possibilités suivantes :

• Choisir la couleur blanche au triangle et non transparente.
• Le premier sommet construit du triangle indique le coin inférieur gauche de l’image. Si l’image n’est pas bien ppositionnée, c’est que le premier point choisi n’est pas le bon. On doit alors faire pivoter la texture en utilisant l’onglet ill be that the wrong point was selected first. This can be mended (for instance by using ’rotate texture co-ordinates’ in the texture-dialogue).

Maintenant, seule la face de la pyramide apparait dans le triangle.

Pour terminer, déplacer les points blancs de l’image dans la texture.

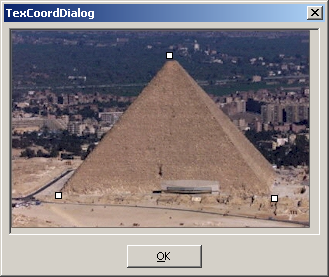
Valider en cliquant sur OK

Remarque : La texture suit les mouvements du triangle

Il est donc possible de représenter une pyramide d’Egypte en 3D.